This video looked into a tricky part of simulating a dice: how to generate random numbers between 1 and 6, all with equal probability. The simple idea of having the computer "spin the wheel" and letting the human choose when it stops turned out to be harder than you might expect.
Section 18 of the datasheet has far more than you want to know about I/O ports. Section 18.4.10 is where PIND is covered (very lightly).
One very important thing introduced in this video is the ASCII encoding of text characters, and the fact that this is how the terminal (keyboard and screen) deals with bytes.
Here is the first version of the code.
0 MOV #6,R1 1 BIT #0x80,PIND 2 JNE 6 3 SUB #1,R1 4 JNE 1 5 JMP 0 6 ADD #'0',R1 7 OUT R1,R1 8 JMP 0
As noted in the video, the loop spans slots 0 to 5. Most times through, only the four instructions between slots 1 and 4 are visited, but when it's wrapping around to start again, it executes all six instructions. This means a wider window — 50% wider — for the button press to occur when six is going to be the answer. This is reflected reasonably well in the figures I got:
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| 28 | 23 | 27 | 28 | 28 | 45 |
Feel free to try it for yourself. If you want to make counting them easier, you might work out how to output a comma after each roll so you end up with a line of numbers ready to paste into a spreadsheet or whatever.
The "clever" tweak to the code was to invert the sense of the test at slot 4.
0 MOV #6,R1 1 BIT #0x80,PIND 2 JNE 6 3 SUB #1,R1 4 JEQ 0 5 JMP 1 6 ADD #'0',R1 7 OUT R1,R1 8 JMP 0
The loop in this version has five instructions in all cases. Most frequently looping between slots 1 and 5, but between 0 and 4 when it wraps.
This is why I said what I did about optimised code. The optimiser recognises loops, and expects them to be executed multiple times. It's reasonable to expect better performance by taking code out of the centre of the loop and moving it to the end cases. (I'm in that habit too, which is why I coded it as I did in the first place)
It's right too. If you count up the loops: in Dice6 there are 5×4 + 6 = 26 instructions for a complete cycle, in Dice6tweaked 6×5 = 30 instructions for a complete cycle. That means that, though the second version is better for our purposes, an optimiser would consider it worse.
The reason I don't fancy this approach is that we've only matched up the number of instructions. ArdEx instructions are all around 10 µs, so it's grudgingly ok, but most processors have some instructions that take two or three times as long as others. The only way to be sure to balance the dice is to use exactly the same instructions every time through the loop.
Easiest way is to just go on counting and let the counter wrap automatically at 256. Only work out which face it was on after the button has been pressed.
20 BIT #128,PIND 21 JNE 24 22 ADD #1,R1 23 JMP 20 24 SUB #6,R1 25 JNC 24 26 ADD #0x37,R1 27 OUT R1,R1 28 WAIT 5000 29 JMP 20
The counting loop is always those first four instructions; it only
escapes to slot 24 when the button press is detected. Slots 24 and 25
work out the remainder when dividing by six. Remember, the carry flag
is set when a subtraction requires a borrow, so when there IS a carry,
the number we started with must have been less than six.
Disappointing that this solution also has a bias, but it's much less than the first one. In counting from 0 to 255, faces 1 to 4 get 43 loops each, 5 and 6 get 42.
It's equivalent to this wheel of fortune. Do 5 and 6 look smaller than the rest to you?
Out of interest, I ran some simulations in the R statistics package. Running 10,000 samples, any bias was still pretty subtle. At 100,000 samples it started looking suspicious. At 1,000,000 samples the bias was very obvious.
Here's how I simulated 100,000 Dice256 rolls in R, in case you're interested.
x<-floor(runif(100000,0,256))%%6 barplot(table(x))
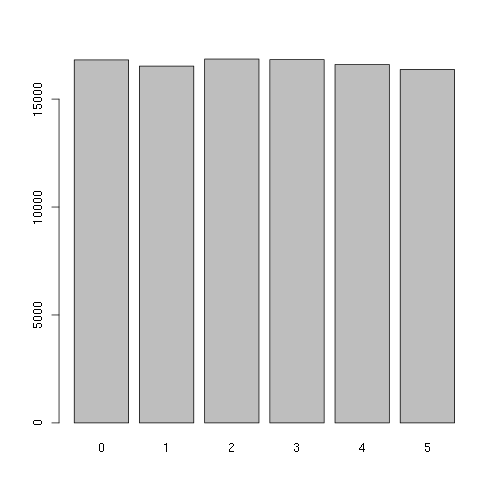
That's how a simulated 100,000 rolls tallied up. The bias was more obvious in other runs.
The video mentioned linear congruential random number generators, as one of the common ways computers generate "random" numbers. If we'd used one of these, there would have been no problem getting a nice even spread from 1 to 6. Why not just go with that?
The best reason is that it's far more interesting this way.
The technical reason is that a dice generates truly random numbers. An LCG algorithm (or any other algorithm that works with a seed value) can only generate fixed sequences of numbers. These sequences can be very useful, but they are not random at all.
If an algorithm has a 32-bit seed, there are only 232 (about 4 billion) possible sequences (i.e. the sequence starting with seed=1, the sequence starting with seed=2, etc.). That is not quite enough to be able to simulate every possible outcome of 13 rolls of a dice (613 is just over 13 billion). Similarly, it couldn't simulate all possibilities drawing six cards from a deck (52×51×50×49×48×47 is about 14.6 billion). A 64-bit seed couldn't cover all possible sequences of 25 dice rolls.
While Dice256 suffers from a small bias away from 5 and 6, at least it allows the tiny but real possibility of rolling 25 twos in a row (along with any other sequence).
The video suggested you write the LED handler, the other main task for the dice simulator.
The video also drew your attention to the BIS (bit set) and SL (shift left) instructions. These, along with what you have already seen, will be enough to knock this task over. Look them up in the instruction reference.
You can compare yours with mine in the next video.